ARTICo³ – Floating Point Arithmetic

Tutorial created on July 9, 2019 by A. Rodríguez

In this tutorial, you will use a block-based algorithm to multiply 512x512 matrices (32-bit single precision floating point) using accelerators capable of multiplying 64x64 matrices (32-bit single precision floating point).

This tutorial covers the following topics:

Using floating point data in ARTICo³ accelerators
Working with hardware redundancy in ARTICo³

Requirements

First Steps

Basic Implementation

IMPORTANT: this tutorial builds on top of the solution of the previous one (Hello, World!). Although it is not strictly necessary to finish it before (the solution is provided as input), it is highly advisable to do so.

In this tutorial, you will be using two new ARTICo³ functions that perform data type conversion:

a3tof: to convert from a3data_t (native ARTICo³ data type) to single precision floating point
ftoa3: to convert from single precision floating point to a3data_t (native ARTICo³ data type)

Set Up Workspace

Download the project from here and extract the files.

Modify Accelerator Code

Open matmul/src/a3_matmul/hls/matmul.cpp, which is the file that contains the C code of the ARTICo³ accelerator.

Change the ARTICo³ kernel definition to match the following code:

A3_KERNEL(a3in_t a, a3in_t b, a3out_t c) {
    uint8_t i, j, k;
    float aux;
    for (i = 0; i < SIZE; i++) {
        for (j = 0; j < SIZE; j++) {
            aux = 0;
            for (k = 0; k < SIZE; k++) {
                aux += a3tof(a[i*SIZE + k]) * a3tof(b[k*SIZE + j]);
            }
            c[i*SIZE + j] = ftoa3(aux);
        }
    }
}

Data interfaces in ARTICo³ are forced have the a3data_t data type. Hence, local variables (e.g., aux) and data conversion functions have been added to ensure proper behavior in the generated accelerators.

Modify Application Code

Open matmul/src/application/main.c, which is the file that contains the C code of the host application.

Modify the input definitions to match the following code:

// Allocate memory
float *A = malloc(512 * 512 * sizeof *A);
float *B = malloc(512 * 512 * sizeof *B);
float *C_sw = malloc(512 * 512 * sizeof *C_sw);
float *C_hw = malloc(512 * 512 * sizeof *C_hw);
// Initialize inputs
srand(time(NULL));
for (i = 0; i < (512 * 512); i++) {
    A[i] = 1.0 + sqrt(rand() / 1000.0);
    B[i] = 20.0 + sin(rand() / 1000.0);
}

Modify data copies between application memories and shared buffers:

// Copy partial inputs
for (k = 0; k < 512; k+=64) {
    for (i2 = 0; i2 < 64; i2++) {
        for (j2 = 0; j2 < 64; j2++) {
            a[((i2 + k) * 64) + j2] = ftoa3(A[((i + i2) * 512) + (k + j2)]);
            b[((i2 + k) * 64) + j2] = ftoa3(B[((k + i2) * 512) + (j + j2)]);
        }
    }
}

// Copy partial output
for (k = 0; k < 512; k+=64) {
    for (i2 = 0; i2 < 64; i2++) {
        for (j2 = 0; j2 < 64; j2++) {
            C_hw[((i + i2) * 512) + (j + j2)] += a3tof(c[((i2 + k)* 64) + j2]);
        }
    }
}

Modify reference software function:

void matmul_sw(int size, float a[size], float b[size], float c[size]) {

Modify how errors are computed:

int errors = 0;
float max_error = 0.0;
for (i = 0; i < (512 * 512); i++) {
    if (fabsf(C_hw[i] - C_sw[i]) > fabsf(1e-5 * C_sw[i])) errors++;
    if (fabsf(C_sw[i]) > FLT_MIN) {
        float error = fabsf((C_hw[i] - C_sw[i]) / C_sw[i]);
        max_error = (error > max_error) ? error : max_error;
    }
}
printf("Found %d errors\n", errors);
printf("Maximum relative error is %g\n", max_error);

IMPORTANT: floating point arithmetic can lead to slightly different results when performing operations in a different order. Hence, it is necessary to include additional checks to see if there are errors between software and hardware computations.

Make sure to include all required headers:

#include <math.h>  // sqrt()
#include <float.h> // FLT_MIN

Build & Run Application

Use the ARTICo³ toolchain to build the project and generate both FPGA bitstreams (export_hw and build_hw) and application executable (export_sw and build_sw). Copy required files to target platform and run the application.

The complete solution of this tutorial can be downloaded from here.

Enabling Hardware Redundancy

Using hardware redundancy in ARTICo³ is easy: you only need to specify how accelerators are grouped during execution using the function artico3_load. In the original version of the application, kernels were loaded using the following code:

for (i = 0; i < 4; i++) {
    artico3_load("matmul", i, 0, 0, 1);
}

This loads all 4 instances of the matmul kernel and configures them to operate in SIMD-like fashion (i.e., without hardware redundancy). If you want to use the accelerators in two DMR groups, change the code to:

artico3_load("matmul", 0, 0, 1, 1);
artico3_load("matmul", 1, 0, 1, 1);
artico3_load("matmul", 2, 0, 2, 1);
artico3_load("matmul", 3, 0, 2, 1);

On the contrary, if you want to enable TMR in your application, change the code to:

artico3_load("matmul", 0, 1, 0, 1);
artico3_load("matmul", 1, 1, 0, 1);
artico3_load("matmul", 2, 1, 0, 1);

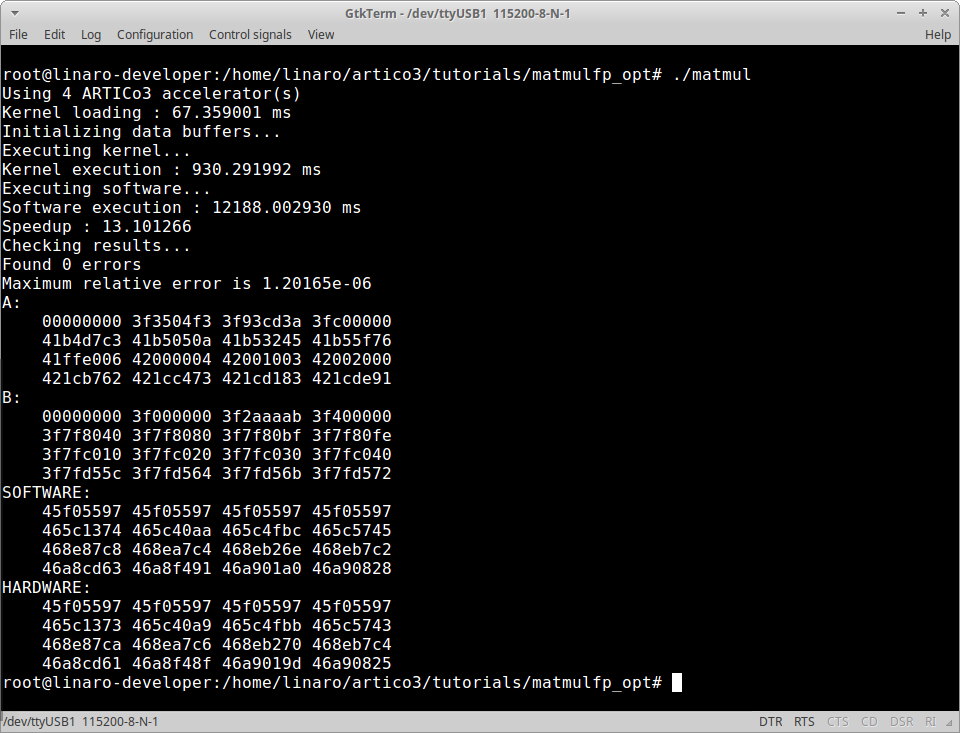
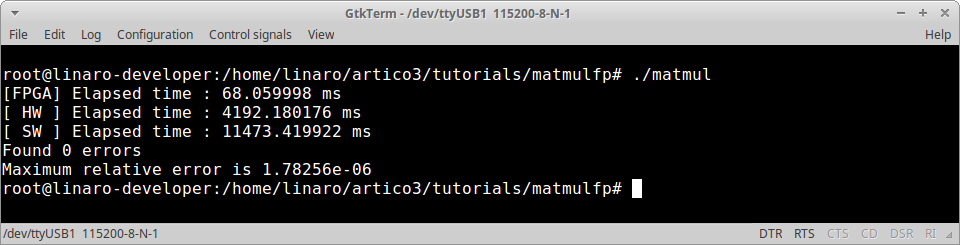
After changing the code, make sure to clean_sw -r (to remove the previous software project), export_sw and build_sw. Then copy the application executable to the target platform and check the results. Pay attention to the elapsed times vs. redundancy level tradeoff when using 4 (no redundancy), 2 (DMR) and 1 (TMR) effective accelerator instances.

IMPORTANT: the last parameter of the artico3_load function can be set to 0 to avoid hardware reconfiguration if the kernel is already loaded in a particular slot. This enables faster configuration changes in the hardware redundancy levels.

Optimized Implementation

The application you have just implemented does not feature any optimization in the hardware accelerators. You can now try and build the artico3/demos/matmul_fp demo, where a block-based matrix multiplication algorithm is also implemented at accelerator level, to check how ARTICo³ can be used to further improve performance.